1796. Диаметр графа
Дан связный
взвешенный неориентированный граф.
Рассмотрим пару
вершин, расстояние между которыми максимально среди всех пар вершин. Расстояние
между ними называется диаметром графа. Эксцентриситетом вершины v называется максимальное расстояние от
вершины v до других вершин графа.
Радиусом графа называется наименьший из эксцентриситетов вершин.
Найдите диаметр
и радиус графа.
Вход. В первой строке находится количество
вершин графа n (1 ≤ n ≤ 100). В следующих n строках по n чисел – матрица смежности графа, где -1 означает отсутствие ребра
между вершинами, а любое неотрицательное число – присутствие ребра данного
веса. На главной диагонали матрицы всегда нули; веса рёбер не превышают 1000.
Выход. Выведите
два числа – диаметр и радиус графа.
|
Пример входа |
Пример выхода |
|
4 0 -1 1 2 -1 0 -1 5 1 -1 0 4 2 5 4
0 |
8 5 |
РЕШЕНИЕ
графы –
алгоритм Флойда - Уоршела
Анализ алгоритма
При помощи
алгоритма Флойда – Уоршела построим матрицу кратчайших расстояний между
вершинами графа. Обозначим через v1,
v2, …, vn вершины графа, d(vi,
vj) – кратчайшее
расстояние между вершинами vi
и vj. Вычислим
r(vi) = ![]()
Тогда
минимальное значение из r(vi) является радиусом графа,
а максимальное – диаметром.
Пример
Граф,
приведенный в условии, имеет вид:
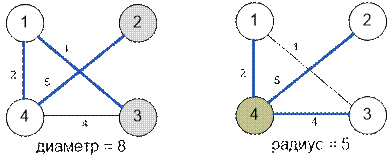
Наибольшее
расстояние между парами вершин (2 и 3) составляет 8 (диаметр графа). Наименьшим
является максимальное расстояние от вершины 4 до других вершин графа и
составляет 5 (радиус графа).
Реализация алгоритма
Объявим константы
и весовую матрицу графа.
#define MAX 110
#define INF 0x3F3F3F3F
int g[MAX][MAX];
Функция floyd реализует
алгоритм Флойда – Уоршела.
void floyd(void)
{
int i, j, k;
for(k = 0; k
< n; k++)
for(i = 0; i
< n; i++)
for(j = 0; j
< n; j++)
if (g[i][k]
+ g[k][j] < g[i][j])
g[i][j] = g[i][k] + g[k][j];
}
Основная часть
программы. Читаем входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%d",&g[i][j]);
if (g[i][j]
< 0) g[i][j] = INF;
}
Запускаем нахождение кратчайших расстояний в графе.
floyd();
Для каждой i-ой
вершины находим максимальное расстояние max
от нее до остальных. Среди всех таких максимумов
находим минимум, равный радиусу графа. Максимум максимумов
равен диаметру графа.
diam = 0; radius
= INF;
for(i = 0; i < n; i++)
{
max = 0;
for(j = 0; j
< n; j++)
if (g[i][j]
> max) max = g[i][j];
if (max >
diam) diam = max;
if (max <
radius) radius = max;
}
Выводим диаметр и радиус графа.
printf("%d\n%d\n",diam,radius);
Java реализация
import java.util.Scanner;
public class Main
{
static final int INF = 0x3F3F3F3F;
static int g[][];
static int n;
static void
floyd()
{
for(int k = 0; k < n; k++)
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
if (g[i][k] + g[k][j] < g[i][j])
g[i][j] = g[i][k] + g[k][j];
}
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
g = new int[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
{
g[i][j] = con.nextInt();
if (g[i][j] < 0) g[i][j] = INF;
}
floyd();
int diam = 0, radius = INF;
for(int i = 0; i < n; i++)
{
int max = 0;
for(int j = 0; j < n; j++)
if (g[i][j] > max) max = g[i][j];
if (max > diam) diam = max;
if (max < radius) radius = max;
}
System.out.println(diam + "\n" + radius);
con.close();
}
}